连续复利 – 金融百科 – 金融知识

连续复利

连续复利(Continuous compounding)

复利就是复合利息，它是指每年的收益还可以产生收益，具体是将整个借贷期限分割为若干段，前一段按本金计算出的利息要加入到本金中，形成增大了的本金，作为下一段计算利息的本金基数，直到每一段的利息都计算出来，加总之后，就得出整个借贷期内的利息，简单来说就是俗称的利滚利。

而连续复利则是指在期数趋于无限大的极限情况下得到的利率，此时不同期之间的间隔很短，可以看作是无穷小量。

设本金为p0 ，年利率为i，当每年含有m个复利结算周期（若一个月为一个复利结算周期，则m=12，若以一季度为一个复利结算周期，则m=4）时，则n年后的本利和为：

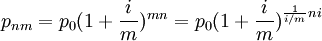
$p_{nm}=p_0(1+frac{i}{m})^{mn}=p_0(1+frac{i}{m})^{frac{1}{i/m}ni}$

当复利结算的周期数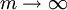 $mto infty$ （这意味着资金运用率最大限度的提高）时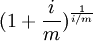， $(1+frac{i}{m})^{frac{1}{i/m}}$ 的极限为e,即

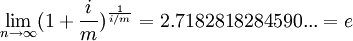
$lim_{n to infty}(1+frac{i}{m})^{frac{1}{i/m}}=2.7182818284590...=e$

所以当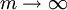 $mto infty$ 连续复利本利和公式为：

$p_n=lim_{m to infty}p_0(1+frac{i}{m})^{mn}=p_0lim_{m to infty}[(1+frac{i}{m})^{frac{1}{i/m}}]^{ni}=p_0e^{ni}$ (1)

即：pn = p0eni

式中eni成为瞬间复利系数，或称一元钱的瞬间复利本利和